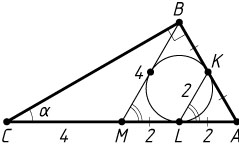
6286. В прямоугольном треугольнике ABC
с прямым углом при вершине B
провели медиану BM
. Окружность, вписанная в треугольник ABM
, касается сторон AB
и AM
в точках K
и L
. Известно, что прямые KL
и BM
параллельны. Найдите угол ACB
.
Ответ. 30^{\circ}
.
Решение. Пусть вписанная окружность треугольника ABM
касается стороны AB
в точке K
, а стороны AM
— в точке L
. Обозначим \angle ACB=\alpha
. Тогда \angle BAC=90^{\circ}-\alpha
.
Их свойства медианы прямоугольного треугольника, проведённой из вершины прямого угла (см. задачу 1109), следует, что BM=MC
. Поэтому
\angle CBM=\angle MCB=\alpha.
По теореме о внешнем угле треугольника
\angle BMC=\angle CBM+\angle MCB=\alpha+\alpha=2\alpha.
Прямые KL
и BM
параллельны, поэтому
\angle ALK=\angle AMB=2\alpha.
Касательные AK
и AM
проведены к окружности из одной точки, поэтому AK=KL
. Из равнобедренного треугольника AKL
находим, что
\angle BAC=\angle KAL=180^{\circ}-2\angle ALK=180^{\circ}-4\alpha.
Из уравнения 180^{\circ}-4\alpha=90^{\circ}-\alpha
находим, что \alpha=30^{\circ}
.