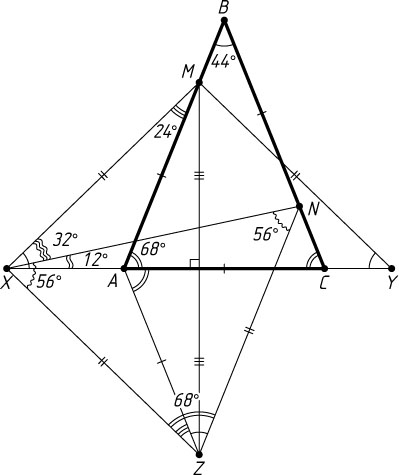
6342. На боковых сторонах AB
и BC
равнобедренного треугольника ABC
с углом 44^{\circ}
при вершине взяты точки M
и N
такие, что AM=BN=AC
. Точка X
на луче CA
такова, что MX=AB
. Найдите угол MXN
.
Ответ. 32^{\circ}
.
Решение. На продолжении основания AC
за точку C
отложим отрезок AY
, равный AB
. Тогда треугольник AYM
равен треугольнику ABC
по двум сторонам и углу между ними (общий угол при вершине A
, AY=AB
по построению, AM=AC
по условию). Значит, \angle AYM=\angle ABC=44^{\circ}
и MY=BC=AB=XM
. Треугольник XMY
— равнобедренный, поэтому \angle YXM=\angle XYM=\angle AYM=44^{\circ}
.
Пусть Z
— точка, симметричная точке M
относительно прямой AC
. Тогда AZ=AM=BN
и
\angle ZAB+\angle ABC=2\angle BAC+\angle ABC=(180^{\circ}-\angle ABC)+\angle ABC=180^{\circ}.
Следовательно, четырёхугольник ABNZ
— параллелограмм.
Тогда ZN=AB=XM=XZ
, значит, треугольник XZN
— равнобедренный. Кроме того, \angle AZN=\angle ABN=44^{\circ}
.
Из равнобедренного треугольника ABC
находим, что
\angle BAC=\frac{1}{2}(180^{\circ}-\angle ABC)=\frac{1}{2}(180^{\circ}-44^{\circ})=68^{\circ}.
По теореме о внешнем угле треугольника
\angle AMX=\angle MAC-\angle YXM=68^{\circ}-44^{\circ}=24^{\circ}.
Тогда
\angle AZX=\angle AMX=24^{\circ},~\angle XZN=\angle AZX+\angle AZN=24^{\circ}+44^{\circ}=68^{\circ}.
Из равнобедренного треугольника XZN
находим, что
\angle ZXN=\frac{1}{2}(180^{\circ}-\angle XZN)=\frac{1}{2}(180^{\circ}-68^{\circ})=56^{\circ},
значит,
\angle CXN=\angle ZXN-\angle ZXC=\angle ZXN-\angle MXC=56^{\circ}-44^{\circ}=12^{\circ}.
Следовательно,
\angle MXN=\angle MXC-\angle CXN=44^{\circ}-12^{\circ}=32^{\circ}.