6352. Дан ромб ABCD
с диагоналями AC=30
и BD=16
. Проведена окружность радиуса 4\sqrt{2}
с центром в точке пересечения диагоналей ромба. Прямая, проходящая через вершину B
, касается этой окружности и пересекает прямую CD
в точке M
. Найдите CM
.
Ответ. \frac{119}{23}
или \frac{391}{7}
.
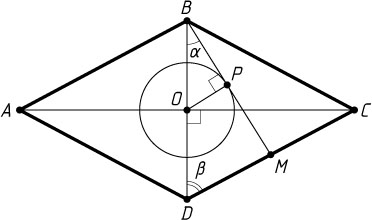
Решение. Пусть точка M
лежит между C
и D
(рис. 1), P
— точка касания прямой BM
с данной окружностью, O
— центр ромба.
По теореме Пифагора
CD=\sqrt{OD^{2}+OC^{2}}=\sqrt{8^{2}+15^{2}}=17.
Обозначим \angle OBM=\alpha
, \angle BDC=\beta
. Из прямоугольных треугольников OPB
и COD
находим, что
\sin\alpha=\frac{OP}{OB}=\frac{4\sqrt{2}}{8}=\frac{\sqrt{2}}{2},~\alpha=45^{\circ},
\cos\beta=\frac{OD}{CD}=\frac{8}{17},~\sin\beta=\frac{15}{17}.
Применяя теорему синусов к треугольнику BMD
получим, что \frac{DM}{\sin\angle MBD}=\frac{BD}{\sin\angle BMD}
, поэтому
MD=\frac{BD\sin\angle MBD}{\sin\angle BMD}=\frac{16\sin45^{\circ}}{\sin(180^{\circ}-45^{\circ}-\beta)}=\frac{8\sqrt{2}}{\sin(45^{\circ}+\beta)}=
=\frac{8\sqrt{2}}{\sin45^{\circ}\cos\beta+\cos45^{\circ}\sin\beta}=\frac{8\sqrt{2}}{\frac{\sqrt{2}}{2}\cdot\frac{8}{17}+\frac{\sqrt{2}}{2}\cdot\frac{15}{17}}=\frac{272}{23}.
Следовательно,
CM=CD-MD=17-\frac{272}{23}=\frac{119}{23}.
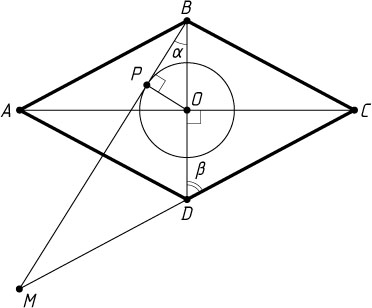
Пусть теперь точка M
лежит на продолжении стороны CD
за точку D
(рис. 2). Тогда по теореме о внешнем угле треугольника \angle BMD=\angle BDC-\angle MBD=\beta-\alpha
. Далее, рассуждая аналогично предыдущему случаю, получим, что
MD=\frac{8\sqrt{2}}{\sin(\beta-45^{\circ})}=\frac{8\sqrt{2}}{\sin\beta\cos45^{\circ}-\sin45^{\circ}\cos\beta}=\frac{8\sqrt{2}}{\frac{\sqrt{2}}{2}\cdot\frac{15}{17}-\frac{\sqrt{2}}{2}\cdot\frac{8}{17}}=\frac{272}{7}.
Следовательно,
CM=CD+MD=17+\frac{272}{7}=\frac{391}{7}.