6451. На сторонах единичного квадрата как на гипотенузах построены во внешнюю сторону прямоугольные треугольники. Пусть A
, B
, C
и D
— вершины их прямых углов, а O_{1}
, O_{2}
, O_{3}
и O_{4}
— центры вписанных окружностей этих треугольников. Докажите, что
а) площадь четырёхугольника ABCD
не превосходит 2;
б) площадь четырёхугольника O_{1}O_{2}O_{3}O_{4}
не превосходит 1.
Указание. Докажите сначала, что площадь четырёхугольника, лежащего в круге радиуса R
не превосходит 2R^{2}
.
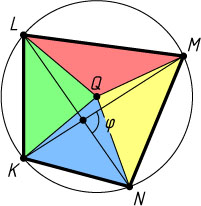
Решение. Докажем сначала вспомогательный факт: площадь четырёхугольника KLMN
, лежащего в круге радиуса R
не превосходит 2R^{2}
.
Пусть Q
— центр круга (рис. 1). Площадь каждого из треугольников QKL
, QLM
, QMN
и QNK
равна половине произведения сторон, исходящих из общей вершины Q
, на синус угла между ними, а значит, не превосходит \frac{1}{2}R^{2}
. Поскольку четыре указанных треугольника покрывают четырёхугольник KLMN
, то его площадь не больше 2R^{2}
.
Другое доказательство этого факта: пусть \varphi
— угол между диагоналями KM
и LN
; тогда
S_{KLMN}=\frac{1}{2}KM\cdot LN\sin\varphi\leqslant\frac{1}{2}\cdot2R\cdot2R\cdot1=2R^{2}.
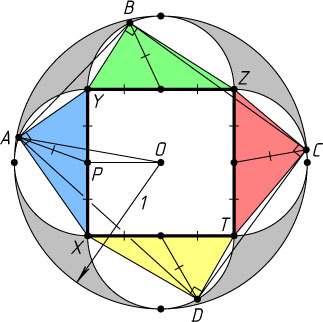
Перейдём к нашей задаче. Пусть O
— центр квадрата XYZT
(рис. 2).
а) Если P
— середина гипотенузы прямоугольного треугольного треугольника AXY
с вершиной прямого угла A
, то
OA\leqslant OP+PA=OP+\frac{1}{2}XY=\frac{1}{2}+\frac{1}{2}=1.
Значит, точка A
лежит внутри круга с центром O
радиуса 1. Аналогично для точек B
, C
и D
. Таким образом, четырёхугольник ABCD
лежит внутри круга радиуса 1. По ранее доказанному его площадь не превосходит 2.
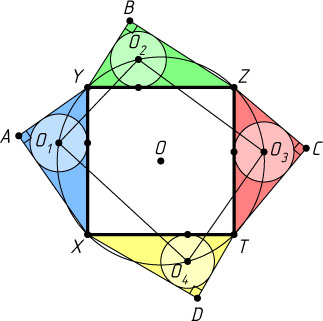
б) Рассмотрим окружность \gamma
, описанную вокруг квадрата XYZT
(её радиус равен \frac{\sqrt{2}}{2}
). Пусть O_{1}
— центр вписанной окружности треугольника XAY
(рис. 3). Поскольку XO_{1}
и YO_{1}
— биссектрисы углов AXY
и AYX
, то
\angle XO_{1}Y=90^{\circ}+\frac{1}{2}\angle XAY=90^{\circ}+45^{\circ}=135^{\circ}
(см. задачу 4770), а так как
\angle XZY+\angle XO_{1}Y=45^{\circ}+135^{\circ}=180^{\circ},
то точка O_{1}
лежит на окружности \gamma
. Аналогично докажем, что точки O_{2}
, O_{3}
и O_{4}
также лежат на окружности \gamma
. Значит, четырёхугольник O_{1}O_{2}O_{3}O_{4}
расположен в круге радиуса \frac{\sqrt{2}}{2}
. Следовательно, его площадь не превосходит 2\left(\frac{\sqrt{2}}{2}\right)^{2}=1
, что и требовалось доказать.