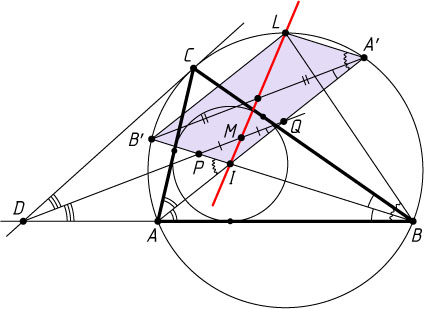
6821. Неравнобедренный треугольник ABC
вписан в окружность \omega
. Касательная к этой окружности в точке C
пересекает прямую AB
в точке D
. Пусть I
— центр окружности, вписанной в треугольник ABC
. Прямые AI
и BI
пересекают биссектрису угла CDB
в точках Q
и P
соответственно. Пусть M
— середина отрезка PQ
. Докажите, что прямая MI
проходит через середину дуги ACB
окружности \omega
.
Решение. Пусть, без ограничения общности, точка D
лежит на луче BA
. Пусть биссектрисы AI
и BI
углов треугольника пересекают \omega
вторично в точках A'
и B'
соответственно. Пусть, наконец, L
— середина дуги ACB
.
Вписанные углы LA'A
и LBA
опираются на одну и ту же дугу AB'L
, равную половине дуги ACB
, а AIB'
— внешний угол треугольника AIB
, поэтому
\angle LA'A=\angle LBA=\frac{1}{2}(\angle A+\angle B)=\frac{1}{2}(\angle IAB+\angle IBA)=\angle B'IA.
Значит, LA'\parallel IB'
. Аналогично LB'\parallel IA'
, поэтому IA'LB'
— параллелограмм, и прямая LI
делит его диагональ A'B'
пополам.
По теореме о внешнем угле треугольника и по теореме об угле между касательной и хордой
\angle CDB=\angle CAB-\angle ACD=\angle CAB-\angle ABC=\angle A-\angle B.
а так как QAB
— внешний угол треугольника ADQ
, то
\angle PQA=\angle QAB-\angle QDA=\frac{1}{2}\angle A-\frac{1}{2}(\angle A-\angle B)=
=\frac{1}{2}\angle B=\angle ABB'=\angle B'A'A,
значит, PQ\parallel A'B'
. Но тогда прямая LI
, делящая отрезок A'B'
пополам, делит пополам и отрезок PQ
(см. задачу 2607). Что и требовалось доказать.