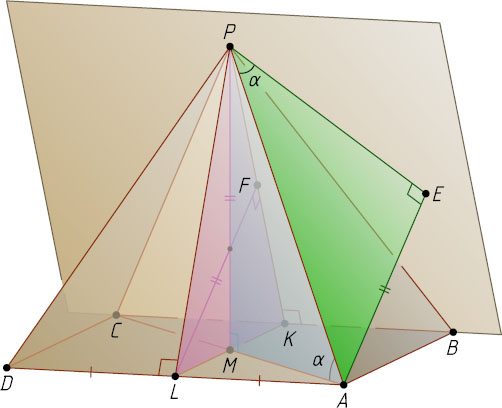
7099. В правильной четырёхугольной пирамиде ABCDP
угол между боковым ребром PA
и плоскостью основания ABCD
равен углу между ребром PA
и плоскостью PBC
. Найдите этот угол.
Ответ. \arctg\sqrt{\frac{3}{2}}=\arccos\sqrt{\frac{2}{5}}
.
Указание. Пусть E
— ортогональная проекция точки A
на плоскость грани BPC
, M
— центр основания. Докажите, что треугольники AEP
и PMA
равны.
Решение. Пусть E
— ортогональная проекция точки A
на плоскость грани BPC
. Тогда \angle APE
— искомый угол. Обозначим его \alpha
. Поскольку прямая AD
параллельна плоскости грани BPC
, все её точки равноудалены от этой плоскости.
Рассмотрим сечение данной пирамиды плоскостью, проходящей через точку P
, середину L
ребра AD
и центр M
основания ABCD
. Эта плоскость перпендикулярна прямым AD
и BC
, поскольку каждая из этих параллельных прямых перпендикулярна PM
(высоте пирамиды) и PL
. Пусть эта плоскость пересекает ребро BC
в точке K
. Тогда PK
— высота и медиана равнобедренного треугольника BPC
. Высота LF
равнобедренного треугольника LPK
перпендикулярна плоскости BPC
, так как она перпендикулярна пересекающимся прямым PK
и BC
этой плоскости. Значит, LF=AE
.
Прямоугольные треугольники AEP
и PMA
равны по гипотенузе (AP
— общая) и острому углу (\angle APE=\angle PAM
по условию задачи), поэтому
PM=AE=LF.
В равнобедренном треугольнике LPK
равны высоты, опущенные на основание и боковую сторону, следовательно, этот треугольник — равносторонний.
Обозначим AD=a
. Тогда
AM=\frac{a\sqrt{2}}{2},~PM=LM\tg\angle PLM=\frac{a}{2}\cdot\tg60^{\circ}=\frac{a\sqrt{3}}{2},
\tg\alpha=\tg\angle PAM=\frac{PM}{AM}=\frac{\frac{a\sqrt{3}}{2}}{\frac{a\sqrt{2}}{2}}=\sqrt{\frac{3}{2}},
\cos\alpha=\sqrt{\frac{2}{5}}.