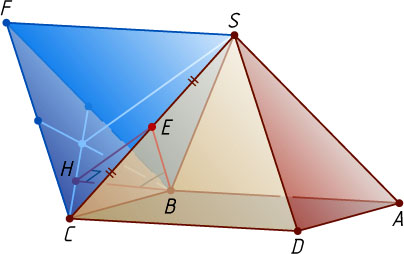
7345. В правильной четырёхугольной пирамиде SABCD
с вершиной S
, все рёбра которой равны, найдите синус угла между прямой BE
и плоскостью SAD
, где E
— середина ребра SC
.
Ответ. \frac{\sqrt{2}}{3}
.
Решение. Пусть рёбра данной пирамиды равны a
, а искомый угол равен \alpha
. Через вершину S
проведём прямую, параллельную AB
и отложим на ней отрезок SF=AB
так, чтобы точки F
и B
лежали по одну сторону от плоскости SAD
. Тогда SABF
— параллелограмм, поэтому BF\parallel AS
и BF=AS=a
. Аналогично CF\parallel SD
и CF=SD=a
.
По признаку параллельности плоскостей плоскость BFC
параллельна плоскости SAD
, поэтому угол между прямой BE
и плоскостью SAD
равен углу между плоскостью BFC
наклонной BE
к этой плоскости.
Пусть H
— проекция точки E
на плоскость BFC
. Тогда отрезок EH
равен половине высоты правильного тетраэдра SBCF
, все рёбра которого равны a
, т. е. EH=\frac{1}{2}a\sqrt{\frac{2}{3}}
, а так как BE
— высота равностороннего треугольника BSC
со стороной a
, то BE=\frac{a\sqrt{3}}{2}
. Следовательно,
\sin\alpha=\sin\angle HBE=\frac{EH}{BE}=\frac{\frac{1}{2}a\sqrt{\frac{2}{3}}}{\frac{a\sqrt{3}}{2}}=\frac{\sqrt{2}}{3}.