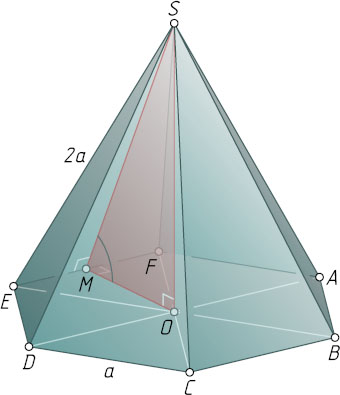
7388. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите косинус угла между плоскостями ABC
и SEF
, если известно, что сторона основания вдвое меньше бокового ребра.
Ответ. \frac{1}{\sqrt{5}}
.
Решение. Пусть O
— центр правильного шестиугольника ABCDEF
, M
— середина стороны EF
. Поскольку OM\perp EF
и SM\perp EF
, угол OMS
— линейный угол двугранного угла между плоскостями ABCDEF
и SEF
.
Положим EF=a
, SE=2a
. Из прямоугольного треугольника SME
находим, что
SM=\sqrt{SE^{2}-ME^{2}}=\sqrt{4a^{2}-\frac{a^{2}}{4}}=\frac{a\sqrt{15}}{2}.
Следовательно,
\cos\angle OMS=\frac{OM}{SM}=\frac{\frac{a\sqrt{3}}{2}}{\frac{a\sqrt{15}}{2}}=\frac{1}{\sqrt{5}}.