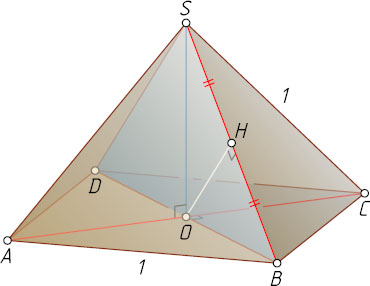
7396. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны 1, найдите расстояние между прямыми SB
и AC
.
Ответ. \frac{1}{2}
.
Решение. Пусть H
— основание перпендикуляра, опущенного из центра основания ABCD
пирамиды на боковое ребро SB
. Прямая AC
перпендикулярна двум пересекающимся прямым BD
и SO
плоскости BSD
, поэтому прямая AC
перпендикулярна этой плоскости. Значит, AC\perp OH
, и OH
— общий перпендикуляр скрещивающихся прямых SB
и AC
. Следовательно, расстояние между этими прямыми равно длине отрезка OH
.
В прямоугольном треугольнике SOB
известно, что
SB=1,~OB=\frac{1}{2}BD=\frac{\sqrt{2}}{2},~SO=\sqrt{SB^{2}-OB^{2}}=\sqrt{1-\left(\frac{\sqrt{2}}{2}\right)^{2}}=\frac{\sqrt{2}}{2}.
Отрезок OH
— высота, а значит, медиана равнобедренного прямоугольного треугольника SOB
, поэтому
OH=\frac{1}{2}SB=\frac{1}{2}.