7808. Противоположные рёбра тетраэдра попарно перпендикулярны. Докажите, что общие перпендикуляры каждой пары противоположных рёбер (бивысоты тетраэдра) пересекаются в одной точке.
Решение. Докажем сначала, что если противоположные рёбра AD
и BC
тетраэдра ABCD
перпендикулярны, то высоты тетраэдра, проведённые из вершин B
и C
, пересекаются, причём точка их пересечения лежит на общем перпендикуляре скрещивающихся прямых AD
и BC
.
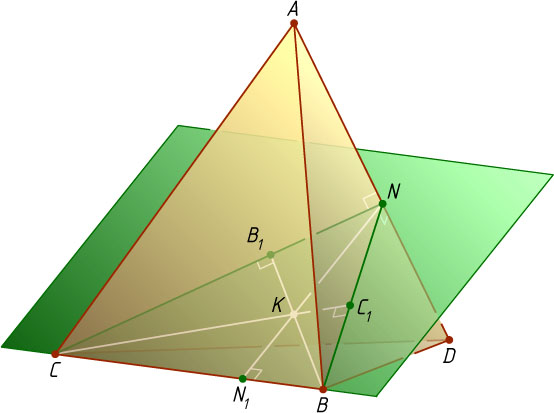
Через прямую BC
проведём плоскость, перпендикулярную прямой AD
. Это можно сделать, так как скрещивающиеся прямые BC
и AD
перпендикулярны. Пусть N
— точка пересечения этой плоскости с прямой AD
. Высота BB_{1}
треугольника BCN
перпендикулярна пересекающимся прямым AD
и CN
плоскости грани ADC
. Значит, BB_{1}
— высота тетраэдра ABCD
. Аналогично, высота CC_{1}
треугольника BCN
также является высотой тетраэдра. Поскольку высоты треугольника пересекаются, пересекаются и прямые BB_{1}
и CC_{1}
.
Пусть K
— точка пересечения BB_{1}
и CC_{1}
. Тогда третья высота NN_{1}
треугольника BCN
проходит через точку K
, а так как NN_{1}
лежит в плоскости, перпендикулярной прямой AD
, то NN_{1}
— общий перпендикуляр скрещивающихся прямых BC
и AD
.
Вернёмся к нашей задаче. Пусть теперь противоположные рёбра тетраэдра ABCD
попарно перпендикулярны. Тогда все его высоты пересекаются в одной точке, причём, по доказанному, эта точка лежит на общем перпендикуляре каждой пары скрещивающихся рёбер. Следовательно, эти общие перпендикуляры пересекаются в одной точке.
Примечание. См. также статью В.Э.Матизена и В.Н.Дубровского: «Из геометрии тетраэдра», Квант, 1988, N9, с.66.
