8242. В пространстве взяты точки A
, B
, C
и D
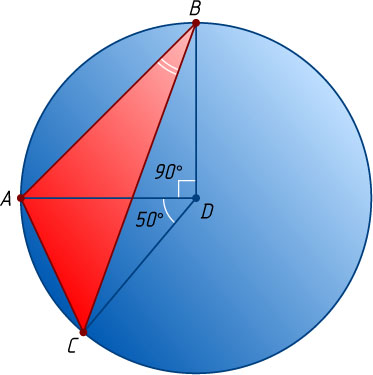
, для которых AD=BD=CD
, \angle ADB=90^{\circ}
, \angle ADC=50^{\circ}
, \angle BDC=140^{\circ}
. Найдите углы треугольника ABC
.
Ответ. 25^{\circ}
, 45^{\circ}
, 110^{\circ}
.
Решение. Предположим, что точки A
, B
, C
и D
не лежат в одной плоскости. Тогда плоские углы трёхгранного угла ABCD
с вершиной D
равны 90^{\circ}
, 50^{\circ}
и 140^{\circ}
, что невозможно, так как 90^{\circ}+50^{\circ}=140^{\circ}
, а сумма двух любых плоских углов трёхгранного угла больше третьего. Следовательно, точки A
, B
, C
и D
лежат в одной плоскости, причём луч DA
лежит между лучами DB
и DC
.
Поскольку AD=BD=CD
, точки A
, B
и C
лежат на окружности с центром D
. Поэтому углы треугольника ABC
— вписанные углы этой окружности. Следовательно,
\angle ABC=\frac{1}{2}\angle ADC=\frac{1}{2}\cdot50^{\circ}=25^{\circ},
\angle ACB=\frac{1}{2}\angle ADB=\frac{1}{2}\cdot90^{\circ}=45^{\circ},
\angle BAC=180^{\circ}-25^{\circ}-45^{\circ}=110^{\circ}.