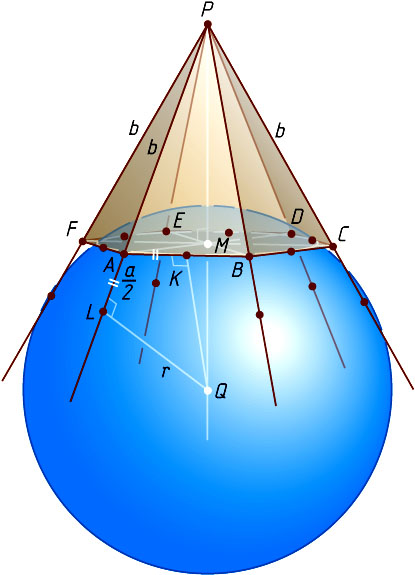
8372. Сторона основания правильной шестиугольной пирамиды равна a
, боковое ребро равно b
. Найдите радиус шара, касающегося сторон основания и продолжений боковых рёбер пирамиды.
Ответ. \frac{a(2b+a)}{2\sqrt{b^{2}-a^{2}}}
.
Решение. Пусть PM
— высота правильной шестиугольной пирамиды PABCDEF
, r
— искомый радиус. Поскольку пирамида правильная, центр Q
указанной сферы лежит на прямой PM
, а точки касания сферы со сторонами основания совпадают с серединами этих сторон. Если K
и L
— точки касания сферы соответственно с ребром AB
и продолжением ребра AP
за точку A
, то
QL\perp AP,~AK=\frac{a}{2},~PL=AP+AL=b+\frac{a}{2}=\frac{2b+a}{2}.
Из прямоугольного треугольника AMP
находим, что
PM=\sqrt{AP^{2}-AM^{2}}=\sqrt{b^{2}-a^{2}}.
Из подобия прямоугольных треугольников PLQ
и PMA
следует, что \frac{QL}{PL}=\frac{AM}{PM}
. Следовательно,
r=QL=PL\cdot\frac{AM}{PM}=\frac{2b+a}{2}\cdot\frac{a}{\sqrt{b^{2}-a^{2}}}=\frac{a(2b+a)}{2\sqrt{b^{2}-a^{2}}}.