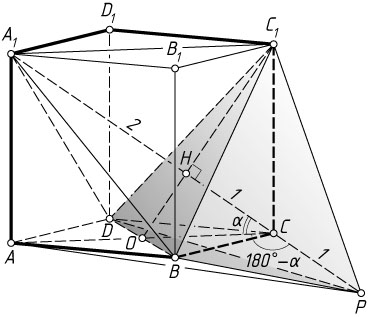
9558. Длина диагонали куба ABCDA_{1}B_{1}C_{1}D_{1}
равна 3. На луче A_{1}C
отмечена точка P
так, что A_{1}P=4
.
а) Докажите, что PBDC_{1}
— правильный тетраэдр.
б) Найдите длину отрезка AP
.
Ответ. \sqrt{11}
.
Решение. а)
Первый способ. Поскольку A_{1}C=AB\sqrt{3}
, а BD=BC_{1}=DC_{1}=AB\sqrt{2}
, то AB=\sqrt{3}
, а BD=BC_{1}=DC_{1}=\sqrt{6}
.
Известно, что диагональ A_{1}C
перпендикулярна плоскости BDC_{1}
, проходит через центр H
равностороннего треугольника BDC_{1}
и делится им в отношении 1:2
, считая от точки C
(см. задачи 7300 и 7212). Значит,
CH=\frac{1}{3}AC_{1}=1,~PH=PC+CH=1+1=2,
а PH
— высота правильной треугольной пирамиды PBDC_{1}
с вершиной P
.
Пусть O
— центр квадрата ABCD
. Тогда
HC_{1}=\frac{2}{3}C_{1}O=\frac{2}{3}\cdot\frac{BD\sqrt{3}}{2}=\frac{2}{3}\cdot\frac{\sqrt{6}\cdot\sqrt{3}}{2}=\sqrt{2}.
Из прямоугольного треугольника PHC_{1}
находим, что
PC_{1}=\sqrt{HC_{1}^{2}+PH^{2}}=\sqrt{2+4}=\sqrt{6}=BD.
Аналогично PB=PD=\sqrt{6}
. Таким образом, все грани пирамиды PBDC_{1}
— правильные треугольники (со стороной \sqrt{6}
). Следовательно, это правильный тетраэдр.
Второй способ. Известно, что диагональ A_{1}C
перпендикулярна плоскости BDC_{1}
, проходит через центр H
равностороннего треугольника BDC_{1}
и делится им в отношении 1:2
, считая от точки C
(см. задачи 7300 и 7212). Значит,
CH=\frac{1}{3}AC_{1}=1,~PH=PC+CH=1+1=2=A_{1}H.
Тогда точка P
симметрична точке A_{1}
относительно плоскости BDC_{1}
, а тетраэдр PBDC_{1}
симметричен правильному тетраэдру A_{1}BDC_{1}
. Следовательно, PBDC_{1}
— также правильный тетраэдр.
б) Точка P
лежит в плоскости AA_{1}C
, так как она лежит на прямой A_{1}C
, лежащей в этой плоскости. Длину отрезка AP
найдём из треугольника APC
.
Обозначим \angle ACA_{1}=\alpha
. Тогда
\angle ACP=180^{\circ}-\alpha,~\cos\alpha=\frac{AC}{A_{1}C}=\frac{\sqrt{6}}{3},~
\cos\angle ACP=\cos(180^{\circ}-\alpha)=-\cos\alpha=-\frac{\sqrt{6}}{3}.
Следовательно,
AP=\sqrt{AC^{2}+CP^{2}-2AC\cdot CP\cos\angle ACP}=
=\sqrt{6+1+2\cdot\sqrt{6}\cdot1\cdot\frac{\sqrt{6}}{3}}=\sqrt{6+1+4}=\sqrt{11}.