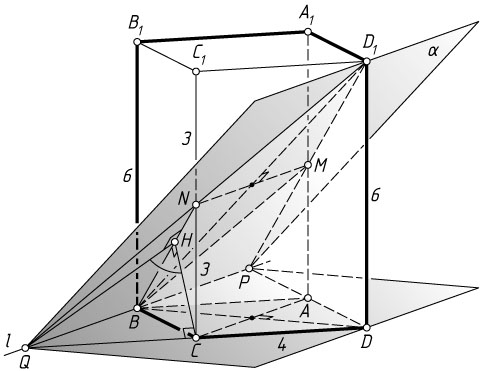
9559. Сечением прямоугольного параллелепипеда ABCDA_{1}B_{1}C_{1}D_{1}
плоскостью \alpha
, содержащей прямую BD_{1}
и параллельной прямой AC
, является ромб.
а) Докажите, что грань ABCD
— квадрат.
б) Найдите угол между плоскостями \alpha
и BCC_{1}
, если AA_{1}=6
, AB=4
.
Ответ. \arctg\frac{5}{3}
.
Решение. а) Плоскость ABCD
проходит через прямую AC
, параллельную плоскости \alpha
, и имеет с плоскостью \alpha
общую точку B
, следовательно, эти плоскости пересекаются по прямой l
, проходящей через точку B
параллельно AC
(см. задачу 8003).
Пусть прямая l
пересекает прямые AD
и CD
в точках P
и Q
соответственно, M
— точка пересечения D_{1}P
и AA_{1}
, N
— точка пересечения D_{1}Q
и CC_{1}
. Тогда сечение параллелепипеда плоскостью \alpha
— ромб BMD_{1}N
.
Поскольку CQ\parallel AB
и BQ\parallel AC
, четырёхугольник ABQC
— параллелограмм, поэтому CQ=AB=CD=C_{1}D_{1}
. Треугольники CNQ
и C_{1}ND_{1}
равны по стороне и двум прилежащим к ней углам, следовательно, N
— середина QD_{1}
. Аналогично докажем, что M
— середина PD_{1}
, поэтому MN
— средняя линия треугольника PD_{1}Q
, MN\parallel PQ\parallel AC
, а так как BD_{1}\perp MN
(как диагонали ромба), то BD_{1}\perp AC
. Тогда по теореме о трёх перпендикулярах BD\perp AC
, т. е. диагонали прямоугольника ABCD
перпендикулярны, следовательно, это квадрат.
б) Плоскости \alpha
и BCC_{1}
пересекаются по прямой BN
, а QC
— перпендикуляр к плоскости BCC_{1}
. Пусть CH
— высота прямоугольного треугольника BCN
. Тогда по теореме о трёх перпендикулярах QH\perp BN
. Значит, CHQ
— линейный угол двугранного угла, образованного плоскостями \alpha
и BCC_{1}
. Тогда (см. задачу 1967)
CH=\frac{BC\cdot CN}{BN}=\frac{BC\cdot CN}{\sqrt{BC^{2}+CN^{2}}}=\frac{4\cdot3}{\sqrt{16+9}}=\frac{12}{5},
\tg\angle CHQ=\frac{CQ}{CH}=\frac{4}{\frac{12}{5}}=\frac{5}{3}.