Игра «Мемори». Пары карточек с картинками перемешивают и раскладывают рубашкой вверх. Игрок открывает карточки по две. Если открытые карточки различны, то они вновь переворачиваются. Цель — как можно быстрее (за наименьшее число ходов) найти все пары.

Видео-лекция об основах алгебры логики и простейших электросхемах. В построении «вычисляющих что-нибудь электросхем» используются «логические кубики», изготовленные старшеклассниками 57 школы для уроков информатики у младших коллег. Лекция снята по просьбе редакции популярного журнала «Квантик». Рассказывает Александр Зайцев.

Интернет-версия листков по планиметрии (подборок задач по разным темам) Рафаила Калмановича Гордина, использующихся на уроках в 57 школе у 8 и 9 классов.

Интернет-версия листков по стереометрии (подборок задач по разным темам) Рафаила Калмановича Гордина, использующихся на уроках в 57 школе у 10 и 11 классов.

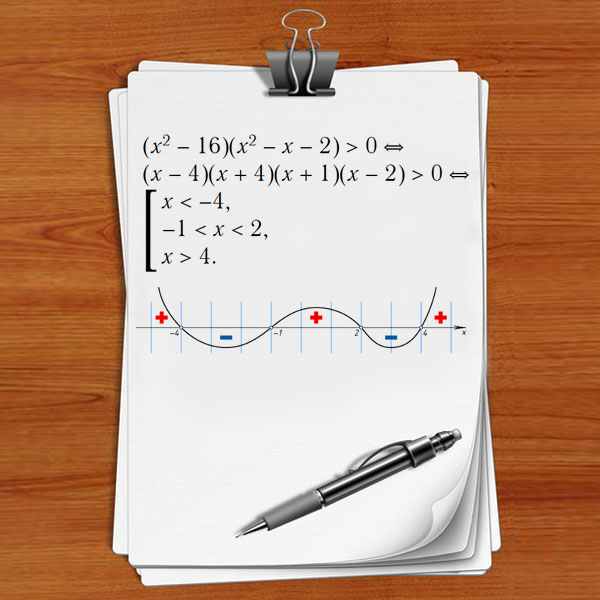Интернет-версия листков по алгебре (подборок задач по разным темам) Рафаила Калмановича Гордина, использующихся на уроках в 57 школе у 9—11 классов.

Кружки по геометрии. До 2020 года каждую неделю в 57 школе под руководством Рафаила Калмановича Гордина проходил кружок по геометрии для школьников. Иногда на них решались оставшиеся неразобранными задачи из программы, иногда выступали приглашённые лекторы или кто-нибудь из самих школьников-участников кружка, но чаще всего просто решались задачи.

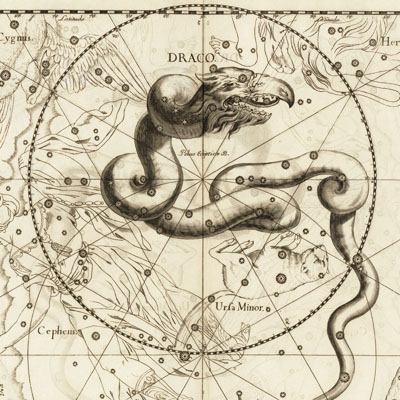Расстояния до звёзд. Диаграммы расположения в пространстве ярчайших звёзд для каждого из 88 созвездий, выполненные с использованием программы METAPOST. К некоторым созвездиям даны гравюры из атласа звёздного неба Яна Гевелия (1690 год). Практика по информатике Ивана Герасимова (10 класс). Помогали Артемий Шведов (11 класс) и М. Панов.

Интернет-версия книги Дмитрия Дмитриевича Ефремова «Новая геометрия треугольника», опубликованной в Одессе в 1902 году. Текст в старой орфографии: с фитами, ятями, десятеричными i. Для интернет-версии были реализованы алгоритм автоматического перевода в современную орфографию (на странице книги кнопка переключения орфографии слева сверху) и алгоритм переносов слов. Планируется (но ещё не доделано) перерисовать все чертежи, снабдив их для понятности несколькими версиями: сначала лишь исходные объекты, затем от слайда к слайду постепенно добавляются все соответствующие дополнительные построения.

Интернет-версия книги Николая Борисовича Васильева и Виктора Львовича Гутенмахера «Прямые и кривые». Предисловие к интернет-версии написал В. Д. Арнольд. Для повторения особого стиля книги («картинки на полях») на javascript реализован алгоритм расстановки переносов в русских словах (колонка текста получается довольно узкой и без переносов тяжко) — теховский стандартный алгоритм с русскими таблицами Вулиса—Львовского. Рисунки взяты из макета изданий МЦНМО. К некоторым рисункам добавлены мультфильмы (которые исходно делались не специально для книги, а в других проектах, так что особой закономерности в них нет; иногда в мультфильме и в тексте не совпадают обозначения точек).

Интернет-версия книги Альфреда Брея Кемпе «Как нарисовать прямую линию?» («How to draw a straight line?») 1877 года. На английском языке. Краткое содержание. Геометрия по Евклиду начинается с аксиом, в которых упоминаются точки и прямые; сразу после них появляется окружность, которую рисуют циркулем — несложным приспособлением из иглы, грифеля и двух палочек произвольной формы. «Рисование» точек тоже не вызывает проблем. А вот чтобы нарисовать прямую, предлагается прибор совершенно иного вида — линейка с прямым краем! Как этот край были изготовлен? Была уже некоторая прямая? Откуда она взялась? Нарисована линейкой?.. Преодолеть этот порочный круг можно, предъявив рисующий отрезки прямых прибор вроде циркуля, для изготовления которого не нужны готовые прямые. Почти на всех рисунках этой книги показаны весьма занятные шарнирные механизмы (точную прямую линию в конце концов удаётся нарисовать!). Для интернет-версии были сделаны мультфильмы, показывающие, как же именно эти механизмы движутся.

Головоломка «Уголки» (или «Складывание полимино») по мотивам одной задачи М. А. Евдокимова. Необходимо сложить из набора уголков прямоугольник. Это не так просто, как кажется! Управление мышью (так что на планшетах использовать не получится): левой кнопкой можно выбирать уголок, параллельный перенос выбранного уголка осуществляется движением мыши, колёсико мыши вращает выбранный уголок, а двойной клик на уголке отражает его относительно горизонтальной оси. По неясным причинам не работает в Firefox. Программа очень легко перенастраивается на фигурки любой формы.

Плакатики по математике для украшения кабинета. Размер 1360×2220 мм (в 14 кабинете 57 школы Москвы — от потолка до уровня парт). По приведённым на странице ссылкам можно скачивать pdf-файлы для заказа таких плакатиков в любой конторе широкоформатной печати (указанных размеров или пропорциональных им). Возможно оставить заявку на изготовление плакатиков и пересылку вам по почте.

Мультфильм «Ну, погоди!», подвергнутый инверсии — геометрическому преобразованию, «выворачивающему» внутренность фиксированной окружности наружу, а наружность этой окружности — внутрь. При инверсии окружности и прямые переходят в окружности и прямые (заметьте: без слова «соответственно»!). Именно это обстоятельство и предлагается увидеть в мультфильме: колёса и провода троллейбуса, границы ступеней эскалатора, поручень лестницы, прямые линии границ телефонной будки, арбузы и многие другие прямые и окружности переходят в прямые и окружности. Можно смотреть прямо на странице (при условии, что браузер поддерживает стандарт HTML5), либо скачать (чуть более качественный) файл в формате avi.