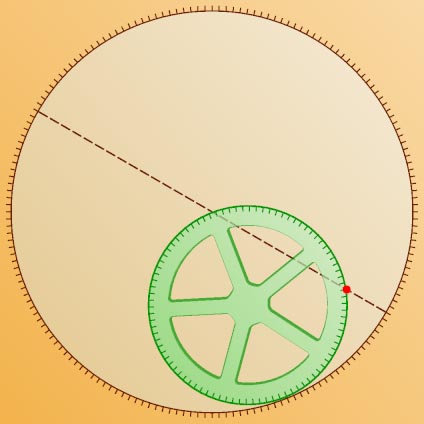
2. Теорема Коперника. По неподвижной окружности, касаясь её изнутри, катится без скольжения окружность вдвое меньшего радиуса. Какую траекторию описывает фиксированная точка K
подвижной окружности?
Ответ. Диаметр окружности.
Указание. Проведите диаметр через первоначальную точку касания.
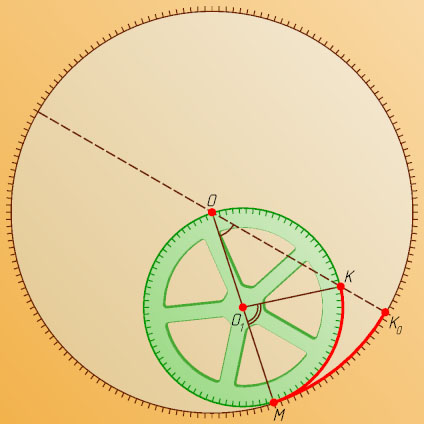
Решение. Пусть O
— центр неподвижной окружности, K_{0}
— первоначальная точка касания окружностей, O_{1}
— новый центр катящейся окружности, M
— новая точка касания, K
— движущаяся точка. Тогда \cup MK_{0}=\cup MK
, поэтому
\angle MO_{1}K=2\angle MOK_{0}.
По теореме о вписанном угле
\angle MO_{1}K=2\angle MOK,
значит, \angle MOK_{0}=\angle MOK
. Следовательно, точка K
лежит на прямой OK_{0}
.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.39, с. 35
Источник: Кюршак Й. и др. Венгерские математические олимпиады. — М.: Мир, 1976. — № 90, с. 23
Источник: Страшевич С., Бровкин Е. Польские математические олимпиады. — М.: Мир, 1978. — № 30, с. 15
Источник: Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М.: Наука, 1978. — с. 8

