3. Хорды AB
и CD
пересекаются в точке M
, лежащей внутри круга. Докажите, что треугольники AMD
и CMB
подобны.
Указание. Угол BAD
равен углу BCD
.
Решение. Поскольку угол BAD
равен углу BCD
(как вписанные углы, опирающиеся на одну и те же дугу), то треугольники AMD
и CMB
подобны по двум углам.
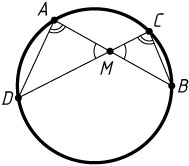
Примечание. Следствие. Произведения отрезков пересекающихся хорд равны между собой.
Действительно, из подобия треугольников AMD
и CMB
следует, что \frac{AM}{CM}=\frac{DM}{BM}
, или AM\cdot BM=CM\cdot DM
.
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — с. 165
