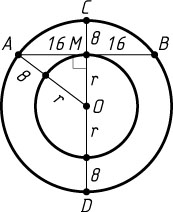
5. В большей из двух концентрических окружностей проведена хорда, равная 32 и касающаяся меньшей окружности. Найдите радиус каждой из окружностей, если ширина образовавшегося кольца равна 8.
Ответ. 12 и 20.
Указание. Примените теорему о произведениях отрезков пересекающихся хорд.
Решение. Пусть O
— центр окружностей, AB
— данная хорда большей окружности, M
— её точка касания с меньшей окружностью, r
— радиус меньшей окружности. Тогда M
— середина AB
(так как OM\perp AB
).
Первый способ. По теореме Пифагора в прямоугольном треугольнике AMO
:
OA^{2}=OM^{2}+MA^{2},~\mbox{или}~(r+8)^{2}=r^{2}+16^{2}.
Из этого уравнения находим, что r=12
.
Второй способ. Проведём диаметр CD
, содержащий точку M
(M
между C
и O
). Тогда
CM\cdot MD=AM\cdot MB,~\mbox{или}~8(2r+8)=16^{2}.
Из этого уравнения находим, что r=12
.
