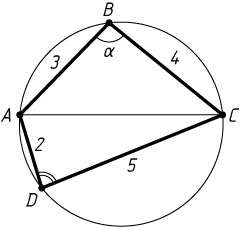
7. Около четырёхугольника ABCD
можно описать окружность. Кроме того, AB=3
, BC=4
, CD=5
и AD=2
. Найдите AC
.
Ответ. \sqrt{\frac{299}{11}}
.
Указание. Примените теорему косинусов и свойство вписанного четырёхугольника.
Решение. Обозначим угол \angle ABC=\alpha
. Тогда
AC^{2}=AB^{2}+BC^{2}-2AB\cdot BC\cos\alpha=AD^{2}+CD^{2}-2AD\cdot CD\cos(180^{\circ}-\alpha),
или
9+16-2\cdot3\cdot4\cos\alpha=4+25+2\cdot2\cdot5\cos\alpha.
Из этого уравнения находим, что \cos\alpha=-\frac{1}{11}
. Следовательно,
AC^{2}=9+16+2\cdot3\cdot4\cdot\frac{1}{11}=\frac{299}{11}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1973, вариант 4
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 84
