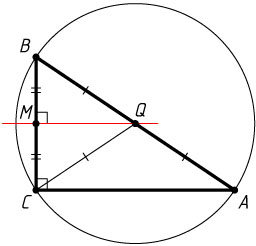
8. Докажите, что центр окружности, описанной около прямоугольного треугольника, совпадает с серединой гипотенузы.
Указание. Рассмотрите точку пересечения серединного перпендикуляра к одному из катетов с гипотенузой треугольника. (Или примените теорему о вписанном угле.)
Решение. Первый способ. Пусть M
— середина катета BC
прямоугольного треугольника ABC
, Q
— точка пересечения серединного перпендикуляра к катету BC
с гипотенузой AB
.
По теореме Фалеса Q
— середина гипотенузы AB
, т. е. QA=QB
. С другой стороны, QC=QA
, так как точка Q
лежит на серединном перпендикуляре к отрезку AC
.
Следовательно, Q
— центр описанной окружности треугольника ABC
.
Второй способ. Вписанный угол измеряется половиной угловой величины дуги, на которую он опирается. Поэтому прямой вписанный угол опирается на диаметр.
Третий способ. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, то середина гипотенузы равноудалена от всех вершин треугольника, т. е. является центром окружности, описанной около треугольника.