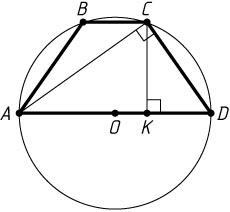
9. Около трапеции ABCD
с основаниями AD
и BC
описана окружность радиуса 6. Центр этой окружности лежит на основании AD
. Основание BC
равно 4. Найдите площадь трапеции.
Ответ. 32\sqrt{2}
.
Указание. Проведите диагональ трапеции.
Решение. Пусть K
— основание перпендикуляра, опущенного из вершины C
на AD
. Тогда
CK^{2}=AK\cdot KD=\frac{1}{2}(AD+BC)\cdot\frac{1}{2}(AD-BC)=8\cdot4.
Поэтому
CK=\sqrt{8\cdot4}=4\sqrt{2}.
Следовательно,
S_{ABCD}=\frac{AD+BC}{2}\cdot CK=32\sqrt{2}.
Примечание. Можно также опустить перпендикуляр из центра окружности на меньшее основание и воспользоваться теоремой Пифагора.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1972 (отделение геофизики), вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 115
