10. В окружность радиуса 2\sqrt{7}
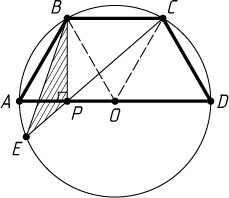
вписана трапеция ABCD
, причём её основание AD
является диаметром, а угол BAD
равен 60^{\circ}
. Хорда CE
пересекает диаметр AD
в точке P
, причём AP:PD=1:3
. Найдите площадь треугольника BPE
.
Ответ. 3\sqrt{3}
.
Указание. BP
— высота трапеции, AP\cdot PD=EP\cdot PC
.
Решение. Пусть O
— центр окружности. Тогда треугольники ABO
, OBC
, COD
— равносторонние, а так как P
— середина AO
, то BP
— высота треугольника ABO
,
BP=AB\sin60^{\circ}=2\sqrt{7}\cdot\frac{\sqrt{3}}{2}=\sqrt{21},~AP=\frac{1}{2}AB=\sqrt{7}.
Поскольку BC=OB=2\sqrt{7}
, то
S_{\triangle BPC}=\frac{1}{2}BC\cdot BP=\frac{1}{2}\cdot2\sqrt{7}\cdot\sqrt{21}=7\sqrt{3}.
По теореме Пифагора
PC=\sqrt{BC^{2}+BP^{2}}=\sqrt{28+21}=7.
По теореме о произведении отрезков пересекающихся хорд AP\cdot PD=EP\cdot PC
. Отсюда находим, что
EP=\frac{AP\cdot PD}{PC}=\frac{\sqrt{7}\cdot3\sqrt{7}}{7}=3.
Следовательно,
S_{\triangle BPE}=\frac{PE}{PC}\cdot S_{\triangle BPC}=\frac{3}{7}\cdot7\sqrt{3}=3\sqrt{3}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1986, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 156
