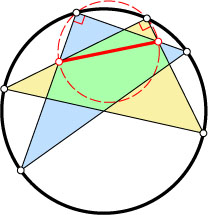
13. В данную окружность впишите прямоугольный треугольник, катеты которого проходили бы через две данные точки внутри окружности.
Указание. Пусть A
и B
— данные точки. На отрезке AB
как на диаметре постройте окружность.
Решение. Если окружность, построенная на отрезке с концами в данных точках как на диаметре, пересекает данную окружность, то каждая точка пересечения — вершина искомого треугольника.
Источник: Кюршак Й. и др. Венгерские математические олимпиады. — М.: Мир, 1976. — № 2, с. 9
Источник: Венгерские математические олимпиады. — 1894, задача 2
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 11, с. 31
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.8, с. 198
