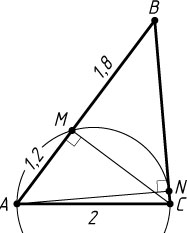
14. В треугольнике ABC
на стороне AC
как на диаметре построена окружность, которая пересекает сторону AB
в точке M
, а сторону BC
— в точке N
. Известно, что AC=2
, AB=3
, AM:MB=2:3
. Найдите AN
.
Ответ. \frac{24}{\sqrt{145}}
.
Указание. AB\cdot CM=BC\cdot AN
.
Решение. Поскольку точки M
и N
лежат на окружности с диаметром AC
, то
\angle AMC=\angle ANC=90^{\circ}.
По теореме Пифагора
MC^{2}=AC^{2}-AM^{2}=2^{2}-\left(\frac{2}{5}\cdot3\right)^{2}=\frac{64}{25},
BC=\sqrt{MC^{2}+BM^{2}}=\sqrt{\frac{64}{25}+\left(\frac{3}{5}\cdot3\right)^{2}}=\frac{\sqrt{145}}{5}.
Поскольку
AB\cdot CM=BC\cdot AN,~\mbox{то}~AN=\frac{AB\cdot CM}{BC}=\frac{24}{\sqrt{145}}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1981, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 71
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.17, с. 40
