16. Дан параллелограмм ABCD
с острым углом при вершине A
. На лучах AB
и CB
отмечены точки H
и K
соответственно, причём CH=BC
и AK=AB
.
а) Докажите, что DH=DK
.
б) Докажите, что треугольники DKH
и ABK
подобны.
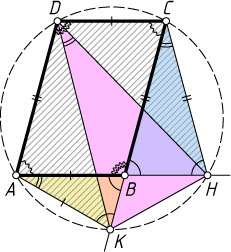
Указание. Треугольник HCD
равен треугольнику DAK
; точки A
, C
, H
, K
лежат на одной окружности. На этой окружности лежит и точка D
.
Решение. Из равенства треугольников HCD
и DAK
(по двум сторонам и углу между ними) следует равенство отрезков DH
и DK
. Из равенства углов KAH
и HCK
следует, что точки A
, C
, H
, K
лежат на одной окружности, а так как
\angle CKA+\angle ADC=180^{\circ},
то на этой окружности лежит и точка D
. Следовательно, углы KAB
и KDH
при вершинах A
и D
равнобедренных треугольников ABK
и DKH
равны. Поэтому треугольники подобны.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.60, с. 37
