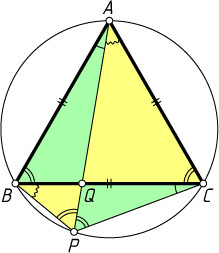
18. На дуге BC
окружности, описанной около равностороннего треугольника ABC
, взята точка P
. Отрезки AP
и BC
пересекаются в точке Q
. Докажите, что \frac{1}{PQ}=\frac{1}{PB}+\frac{1}{PC}
.
Указание. Рассмотрите пары подобных треугольников: BQP
и AQC
, AQB
и CQP
.
Решение. Треугольник BQP
подобен треугольнику AQC
. Поэтому \frac{AC}{BP}=\frac{QC}{PQ}
. Треугольник AQB
подобен треугольнику CQP
. Поэтому \frac{AB}{PC}=\frac{BQ}{PQ}
. Сложив почленно эти два равенства, получим, что
\frac{AC}{BP}+\frac{AB}{PC}=\frac{QC}{PQ}+\frac{BQ}{PQ}=\frac{QC+BQ}{PQ}=\frac{BC}{PQ}.
Поскольку AC=AB=BC
, то
\frac{1}{BP}+\frac{1}{PC}=\frac{1}{PQ}.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.57, с. 36
