19. AA_{1}
и BB_{1}
— высоты треугольника ABC
. Докажите, что:
а) треугольник AA_{1}C
подобен треугольнику BB_{1}C
;
б) треугольник ABC
подобен треугольнику A_{1}B_{1}C
;
в) найдите коэффициент подобия треугольников A_{1}B_{1}C
и ABC
, если \angle ACB=\gamma
.
Ответ. в) |\cos\gamma|
.
Указание. Постройте на стороне AB
как на диаметре окружность.
Решение. Первый способ. а) Прямоугольные треугольники AA_{1}C
и BB_{1}C
подобны по двум углам.
б) Отрезок AB
виден из точек A_{1}
и B_{1}
под прямым углом. Поэтому точки A_{1}
и B_{1}
лежат на окружности с диаметром AB
.
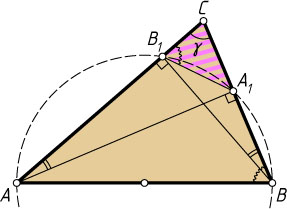
Пусть треугольник ABC
остроугольный. Тогда
\angle ABC=\angle ABA_{1}=180^{\circ}-\angle AB_{1}A_{1}=\angle CB_{1}A_{1}.
Следовательно, треугольники ABC
и A_{1}B_{1}C
подобны по двум углам.
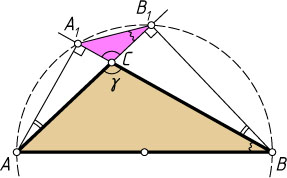
Пусть \angle BAC\gt90^{\circ}
. Тогда вписанные углы AB_{1}A_{1}
и ABA_{1}
опираются на одну и ту же дугу, значит,
\angle CB_{1}A_{1}=\angle AB_{1}A_{1}=\angle ABA_{1}=\angle ABC.
Следовательно, треугольники ABC
и A_{1}B_{1}C
подобны по двум углам. Для случая \angle BAC=90^{\circ}
утверждение очевидно.
Аналогично для случая, когда \angle ABC\geqslant90^{\circ}
.
в) Пусть k
— коэффициент подобия треугольников A_{1}B_{1}C
и ABC
. Тогда, если \gamma\lt90^{\circ}
, то из прямоугольного треугольника CAA_{1}
находим, что
k=\frac{CA_{1}}{CA}=\cos\angle C=\cos\gamma.
Если же \angle ACB\gt90^{\circ}
, то аналогично находим, что
k=\frac{CA_{1}}{CA}=\frac{CB_{1}}{CB}=\cos(180^{\circ}-\angle C)=-\cos\gamma.
Второй способ. а), б) Прямоугольные треугольники AA_{1}C
и BB_{1}C
подобны по двум углам, поэтому \frac{CA_{1}}{CB_{1}}=\frac{CA}{CB}
. Следовательно, треугольники ABC
и A_{1}B_{1}C
подобны по двум сторонам и углу между ними.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 7, с. 73
Источник: Колмогоров А. Н. и др. Геометрия: Учебное пособие для 8 кл. средней школы. — 3-е изд. — М.: Просвещение, 1975. — с. 41
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 4.8, с. 42
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 2, с. 96
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 19, с. 36
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.53, с. 17

