23. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, т. е. если a
, b
и c
— стороны треугольника, а \alpha
, \beta
и \gamma
— противолежащие им углы, то \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}
. При этом, если R
— радиус описанной около треугольника окружности, то
\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2R.
Указание. Пусть A
— рассматриваемый угол. Проведите диаметр окружности через точку B
(или C
).
Решение. Пусть BC=a
, AC=b
, AB=c
— стороны треугольника ABC
, \angle A=\alpha
, \angle B=\beta
, \angle C=\gamma
, O
— центр описанной около треугольника ABC
окружности.
Через точку B
проведём диаметр BA_{1}
. Тогда \angle BCA_{1}=90^{\circ}
.
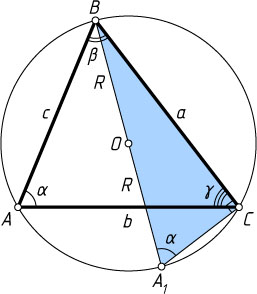
Предположим, что точки A
и O
расположены по одну сторону от прямой BC
(рис. 1). Тогда \angle BA_{1}C=\angle BAC=\alpha
(вписанные углы, опирающиеся на одну и ту же дугу). Из прямоугольного треугольника BCA_{1}
находим, что \frac{a}{\sin\alpha}=2R
.
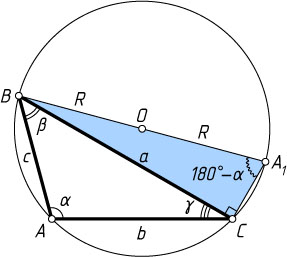
Если точки A
и O
расположены по разные стороны от прямой (рис. 2), то \angle BA_{1}C=180^{\circ}-\angle BAC=180^{\circ}-\alpha
. Из прямоугольного треугольника BCA_{1}
находим, что \frac{a}{\sin(180^{\circ}-\alpha)}=2R
, а так как \sin(180^{\circ}-\alpha)=\sin\alpha
, то \frac{a}{\sin\alpha}=2R
.
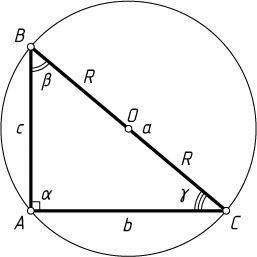
Если же точка O
лежит на отрезке BC
(рис. 3), то \alpha=90^{\circ}
. Значит, \frac{a}{\sin\alpha}=\frac{BC}{\sin90^{\circ}}=BC=2R
.
Аналогично докажем, что \frac{b}{\sin\beta}=2R
и \frac{c}{\sin\gamma}=2R
. Следовательно,
\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2R.
Примечание. Равенство
\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2R
иногда называют обобщённой теоремой синусов (см. Г.С.М.Коксетер, С.Л.Грейтцер. Новые встречи с геометрией. М., «Наука», 1978, с.13).
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 1.54, с. 28
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 13-15
Источник: Погорелов А. В. Геометрия: Учебное пособие для 7—11 кл. средней школы. — 8-е изд. — М.: Просвещение, 1989. — № 11, с. 154
Источник: Колмогоров А. Н. и др. Геометрия: Учебное пособие для 8 кл. средней школы. — 3-е изд. — М.: Просвещение, 1975. — с. 42
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2, с. 289


