24. В окружность вписаны две равнобедренные трапеции с соответственно параллельными сторонами. Докажите, что диагональ одной из них равна диагонали другой трапеции.
Указание. Примените формулу a=2R\sin\alpha
.
Решение. Пусть боковая сторона трапеции образует с меньшим основанием угол \alpha
. Для обеих трапеций этот угол один и тот же, а диагональ равна произведению диаметра окружности на синус этого угла.
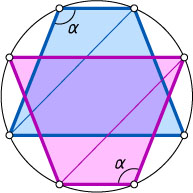
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.32, с. 34
Источник: Турнир городов. — 1987-1988, IX, весенний тур, старшие классы, тренировочный вариант
