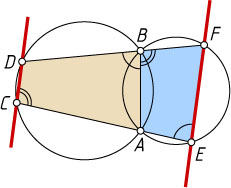
25. Две окружности пересекаются в точках A
и B
. Продолжения хорд AC
и BD
первой окружности пересекают вторую окружность в точках E
и F
соответственно. Докажите, что прямые CD
и EF
параллельны.
Указание. Проведите отрезок AB
.
Решение. Пусть отрезки CE
и FD
не пересекаются. Соединим точки A
и B
. Поскольку
\angle ABD=180^{\circ}-\angle C,~\angle ABF=180^{\circ}-\angle ABD,
то \angle ABF=\angle C
, а так как \angle AEF=180^{\circ}-\angle ABF
, то
\angle CEF+\angle C=180^{\circ}.
Следовательно, CD\parallel EF
.
Аналогично для случая, когда отрезки CE
и FD
пересекаются.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 65, с. 81
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.1, с. 31
Источник: Дынкин Е. Б. и др. Математические задачи. — М.: Наука, 1966. — № 28, с. 11
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 54
