26. Угловые величины противоположных дуг, высекаемых на окружности пересекающимися хордами, равны \alpha
и \beta
. Найдите угол между хордами.
Ответ. \frac{\alpha+\beta}{2}
.
Указание. Соедините концы двух хорд и воспользуйтесь теоремой о внешнем угле треугольника (или через конец одной хорды проведите прямую, параллельную второй хорде).
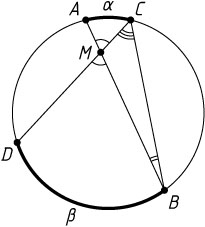
Решение. Пусть угловые величины дуг AC
и BD
, заключённых внутри углов AMC
и BMD
, равны \alpha
и \beta
соответственно. По теореме о внешнем угле треугольника
\angle AMC=\angle MBC+\angle MCB=\angle ABC+\angle DCB=\frac{\alpha}{2}+\frac{\beta}{2}=\frac{\alpha+\beta}{2}.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 78
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1(б), с. 31
Источник: Колмогоров А. Н. и др. Геометрия: Учебное пособие для 8 кл. средней школы. — 3-е изд. — М.: Просвещение, 1975. — с. 41
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 718, с. 180
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 5, с. 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 98
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 13
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 589
