30. Пусть O
— центр окружности, описанной около треугольника ABC
, \angle AOC=60^{\circ}
. Найдите угол AMC
, где M
— центр окружности, вписанной в треугольник ABC
.
Ответ. 165^{\circ}
или 105^{\circ}
.
Указание. AM
и CM
— биссектрисы углов треугольника ABC
.
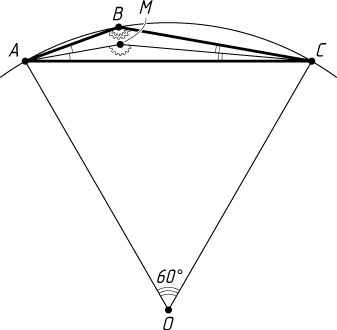
Решение. Если точки O
и B
лежат по разные стороны от прямой AC
(рис. 1), то градусная мера дуги AC
, не содержащей точки B
, равна 360^{\circ}-60^{\circ}=300^{\circ}
, поэтому
\angle ABC=\frac{1}{2}\cdot300^{\circ}=150^{\circ}.
Сумма углов при вершинах A
и C
треугольника ABC
равна 180^{\circ}-150^{\circ}=30^{\circ}
, а так как AM
и CM
— биссектрисы треугольника ABC
, то сумма углов при вершинах A
и C
треугольника AMC
равна 15^{\circ}
. Следовательно,
\angle AMC=180^{\circ}-15^{\circ}=165^{\circ}.
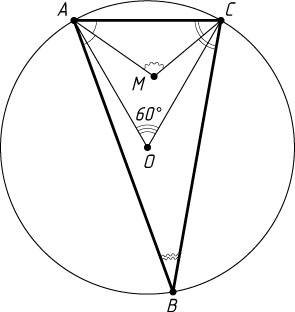
Если же точки O
и B
лежат по одну сторону от прямой AC
(рис. 2), то аналогично получим, что \angle AMC=105^{\circ}
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1973, вариант 4, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 81
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.16, с. 87

