31. Радиус окружности, описанной около остроугольного треугольника ABC
, равен 1. Известно, что на этой окружности лежит центр другой окружности, проходящей через вершины A
, C
и точку пересечения высот треугольника ABC
. Найдите AC
.
Ответ. \sqrt{3}
.
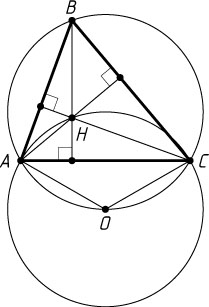
Указание. Пусть H
— точка пересечения высот треугольника ABC
, O
— центр второй окружности. Тогда \angle AHC=180^{\circ}-\angle B
, \angle AOC=2\angle B
.
Решение. Если H
— точка пересечения высот треугольника ABC
, то \angle AHC=180^{\circ}-\angle ABC
. Тогда
\angle AOC=\cup AHC=360^{\circ}-2\angle AHC=2\angle ABC,
где O
— центр второй окружности.
Поскольку \angle AOC+\angle ABC=180^{\circ}
, то 3\angle ABC=180^{\circ}
. Следовательно, \angle ABC=60^{\circ}
. Тогда
AC=2R\sin\angle ABC=2\cdot1\cdot\frac{\sqrt{3}}{2}=\sqrt{3}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1972, вариант 4, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 260
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 220, с. 25
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.39, с. 89
