32. Хорда AB
пересекает противоположные стороны KN
, LM
и диагонали MN
и KL
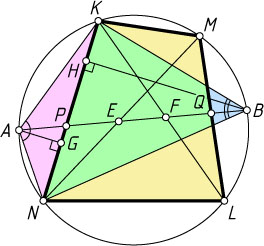
вписанного четырёхугольника KMLN
в точках P
, Q
, E
и F
соответственно. Положим \frac{AP}{PB}=\alpha
, \frac{AQ}{QB}=\beta
, \frac{AE}{EB}=x
, \frac{AF}{FB}=y
. Докажите, что \alpha\beta=xy
.
Решение. Пусть AG
и BH
— высоты треугольников AKN
и BKN
, опущенные на общее основание KN
. Тогда \frac{AG}{BH}=\frac{AP}{BP}
, поэтому \frac{S_{\triangle AKN}}{S_{\triangle BKN}}=\frac{AP}{BP}
. С другой стороны
\frac{S_{\triangle AKN}}{S_{\triangle BKN}}=\frac{\frac{1}{2}AK\cdot AN\sin\angle KAN}{\frac{1}{2}BK\cdot BN\sin\angle KBN}=\frac{AK\cdot AN}{BK\cdot BN}.
Следовательно, \alpha=\frac{AP}{PB}=\frac{AK\cdot AN}{BK\cdot BN}
.
Аналогично докажем, что
\beta=\frac{AQ}{QB}=\frac{AM\cdot AL}{BM\cdot BL},~x=\frac{AE}{EB}=\frac{AL\cdot AN}{BL\cdot BN},~y=\frac{AF}{FB}=\frac{AK\cdot AM}{BK\cdot BM},
значит,
\alpha\beta=\frac{AK\cdot AN}{BK\cdot BN}\cdot\frac{AM\cdot AL}{BM\cdot BL}=\frac{AK\cdot AN\cdot AM\cdot AL}{BK\cdot BN\cdot BM\cdot BL},
xy=\frac{AL\cdot AN}{BL\cdot BN}\cdot\frac{AK\cdot AM}{BK\cdot BM}=\frac{AK\cdot AN\cdot AM\cdot AL}{BK\cdot BN\cdot BM\cdot BL}.
Следовательно, \alpha\beta=xy
.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 1028, с. 126
