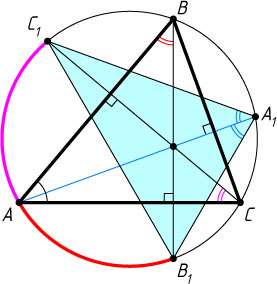
34. Продолжения высот остроугольного треугольника ABC
пересекают описанную окружность в точках A_{1}
, B_{1}
и C_{1}
соответственно. Докажите, что биссектрисы треугольника A_{1}B_{1}C_{1}
лежат на прямых AA_{1}
, BB_{1}
, CC_{1}
.
Указание. \angle ACC_{1}=\angle ABB_{1}
.
Решение. Дуги AC_{1}
и AB_{1}
равны, так как на них опираются равные вписанные углы ACC_{1}
и ABB_{1}
(каждый из них в сумме с углом BAC
составляет 90^{\circ}
). Следовательно,
\angle AA_{1}C_{1}=\angle AA_{1}B_{1},
т. е. луч A_{1}A
— биссектриса угла C_{1}A_{1}B_{1}
. Остальное аналогично.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.7, с. 16
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.20(б), с. 33
