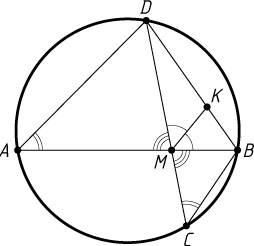
36. В круге проведены две хорды AB
и CD
, пересекающиеся в точке M
; K
— точка пересечения биссектрисы угла BMD
с хордой BD
. Найдите отрезки BK
и KD
, если BD=3
, а площади треугольников CMB
и AMD
относятся как 1:4
.
Ответ. 1 и 2.
Указание. Площади подобных треугольников относятся как квадраты соответствующих сторон.
Решение. Треугольники BMC
и DMA
подобны (\angle MCB=\angle DCB=\angle DAB=\angle DAM
). Поскольку площади этих треугольников относятся как 1:4
, то коэффициент подобия равен \frac{1}{2}
. Поэтому DM=2BM
.
Поскольку MK
— биссектриса треугольника BMD
, то
\frac{DK}{KB}=\frac{DM}{BM}=2.
Следовательно,
DK=\frac{2}{3}BD=2,~BK=\frac{1}{3}BD=1.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1975, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 105
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.10, с. 111
