39. На катете BC
прямоугольного треугольника ABC
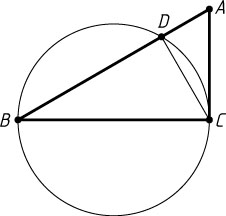
как на диаметре построена окружность, пересекающая гипотенузу в точке D
так, что AD:BD=1:3
. Высота, опущенная из вершины C
прямого угла на гипотенузу, равна 3. Найдите катет BC
.
Ответ. 6.
Указание. CD
— высота треугольника ACD
.
Решение. Поскольку угол BDC
вписан в указанную окружность и опирается на её диаметр BC
, то \angle BDC=90^{\circ}
. Поэтому CD
— высота треугольника ABC
.
Обозначим AD=x
, BD=3x
. Поскольку CD^{2}=AD\cdot DB
, то 3x^{2}=9
. Отсюда находим, что x^{2}=3
. Следовательно,
BC^{2}=CD^{2}+BD^{2}=9+9x^{2}=9+27=36,
а BC=6
.
Источник: Вступительный экзамен на географический факультет МГУ. — 1979, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 70
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 5, задача 1
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1, с. 168
