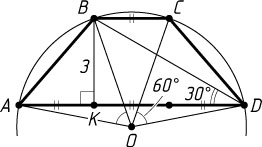
41. Четырёхугольник ABCD
вписан в окружность с центром O
, \angle BOA=\angle COD=60^{\circ}
. Перпендикуляр BK
, опущенный из вершины B
на сторону AD
, равен 6; BC
в три раза меньше AD
. Найдите площадь треугольника COD
.
Ответ. \frac{63\sqrt{3}}{4}
.
Указание. ABCD
— равнобедренная трапеция, \angle BDA=30^{\circ}
.
Решение. Поскольку меньшие дуги AB
и CD
равны, BC\parallel AD
. Поэтому ABCD
— равнобедренная трапеция. По теореме о вписанном угле
\angle BDA=\frac{1}{2}\angle AOB=30^{\circ}.
Из прямоугольного треугольника BKD
находим, что
KD=BK\ctg30^{\circ}=6\sqrt{3}.
С другой стороны,
KD=\frac{1}{2}(BC+AD)=\frac{1}{2}(BC+3BC)=2BC.
Из равенства 2BC=6\sqrt{3}
следует, что BC=3\sqrt{3}
. Тогда
AD=9\sqrt{3},~AK=\frac{1}{2}(AD-BC)=3\sqrt{3},
а так как
OB=OA=AB=\sqrt{BK^{2}+AK^{2}}=\sqrt{36+27}=3\sqrt{7},
то
S_{\triangle COD}=S_{\triangle AOB}=\frac{1}{2}OA\cdot OB\sin\angle AOB=\frac{1}{2}\cdot(3\sqrt{7})^{2}\sin60^{\circ}=\frac{63\sqrt{3}}{4}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1981, вариант 2, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 63
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.25, с. 31
