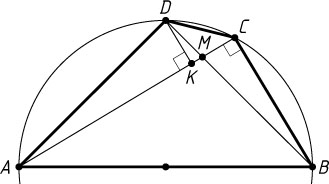
43. В окружность вписан четырёхугольник ABCD
, причём AB
является диаметром окружности. Диагонали AC
и BD
пересекаются в точке M
. Известно, что BC=3
, CM=\frac{3}{4}
, а площадь треугольника ABC
втрое больше площади треугольника ACD
. Найдите AM
.
Ответ. \frac{17}{4}
.
Указание. Пусть DK
— высота треугольника ADC
. Тогда DK=\frac{1}{3}BC
, а треугольник DKM
подобен треугольнику BCM
с коэффициентом \frac{1}{3}
.
Решение. Пусть DK
— высота треугольника ADC
. Поскольку вписанный угол ACB
опирается на диаметр AB
, то \angle ACB=90^{\circ}
. Поэтому DK
параллельно BC
, а так как площадь треугольника ADC
в три раза меньше площади треугольника ABC
, то его высота DK
втрое меньше высоты BC
треугольника ABC
. Следовательно, треугольник DKM
подобен треугольнику BCM
с коэффициентом \frac{1}{3}
.
BM=\sqrt{BC^{2}+CM^{2}}=\frac{3\sqrt{17}}{4},~DM=\frac{1}{3}BM=\frac{\sqrt{17}}{4}.
Поскольку AM\cdot MC=DM\cdot MB
, то
AM=\frac{DM\cdot MB}{MC}=\frac{17}{4}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1975, вариант 4, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 106
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.11, с. 93
