46. Трапеция с высотой h
вписана в окружность. Боковая сторона трапеции видна из центра окружности под углом 120^{\circ}
. Найдите среднюю линию трапеции.
Ответ. \frac{h}{\sqrt{3}}
.
Указание. Проведите через вершину меньшего основания трапеции прямую, параллельную одной из диагоналей, или воспользуйтесь тем, что проекция диагонали равнобедренной трапеции на большее основание равна средней линии трапеции.
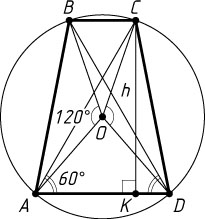
Решение. Первый способ. Пусть O
— центр окружности, описанной около трапеции ABCD
с основаниями AD\gt BC
. Поскольку трапеция равнобедренная, то
AC=BD,~\angle CAD=\angle BDA=\frac{1}{2}\angle BOA=60^{\circ}.
Через вершину C
проведём прямую, параллельную BD
, до пересечения с продолжением AD
в точке K
. Тогда ACK
— равносторонний треугольник,
AK=2h\cos60^{\circ}=\frac{2h}{\sqrt{3}}.
Следовательно, средняя линия трапеции ABCD
равна
\frac{AD+BC}{2}=\frac{AD+DK}{2}=\frac{1}{2}AK=\frac{h}{\sqrt{3}}.
Второй способ. Пусть O
— центр окружности, описанной около трапеции ABCD
с основаниями AD\gt BC
. Поскольку трапеция равнобедренная, то
\angle CAD=\angle BDA=\frac{1}{2}\angle BOA=60^{\circ}.
Пусть CK
— высота трапеции, тогда
AK=h\ctg60^{\circ}=\frac{h}{\sqrt{3}},
но AK
равно средней линия трапеции ABCD
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.22, с. 31
