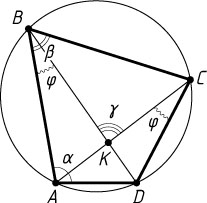
47. Во вписанном четырёхугольнике ABCD
известны углы: \angle DAB=\alpha
, \angle ABC=\beta
, \angle BKC=\gamma
, где K
— точка пересечения диагоналей. Найдите угол ACD
.
Ответ. \frac{\beta+\gamma-\alpha}{2}
.
Указание. Выразите углы треугольника AKB
через \alpha
, \beta
, \gamma
и искомый угол.
Решение. Обозначим \angle ABD=\angle ACD=\varphi
. Тогда
\angle DBC=\beta-\varphi,~\angle CAD=\angle DBC=\beta-\varphi,
\angle BAC=\angle BAD-\angle CAD=\alpha-(\beta-\varphi),
\gamma=\angle BKC=\angle BAC+\angle ABD=(\alpha-\beta+\varphi)+\varphi=\alpha-\beta+2\varphi.
Следовательно,
\varphi=\frac{\beta+\gamma-\alpha}{2}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 79, с. 13
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 79, с. 11
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.13, с. 104
