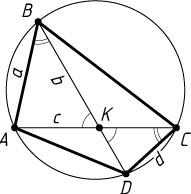
48. Во вписанном четырёхугольнике ABCD
, диагонали которого пересекаются в точке K
, известно, что AB=a
, BK=b
, AK=c
, CD=d
. Найдите AC
.
Ответ. \frac{ac+bd}{a}
.
Указание. Треугольник ABK
подобен треугольнику DCK
.
Решение. Из подобия треугольников ABK
и DCK
(по двум углам) следует, что
\frac{AB}{CD}=\frac{BK}{CK}.
Поэтому
CK=CD\cdot\frac{BK}{AB}=\frac{db}{a}.
Следовательно,
AC=AK+KC=c+\frac{db}{a}=\frac{ac+bd}{a}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 80, с. 13
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 80, с. 11
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.2, с. 93
