49. Докажите, что около четырёхугольника, сумма противоположных углов которого равна 180^{\circ}
, можно описать окружность.
Указание. Проведите окружность через три вершины и докажите, что четвёртая также попадёт на эту окружность.
Решение. Пусть ABCD
— данный четырёхугольник и \angle BAD+\angle BCD=180^{\circ}
. Опишем окружность около треугольника ABD
. Если точка C
окажется на этой окружности, то утверждение доказано.
Первый способ. Пусть точка C
находится внутри окружности. Продолжим луч DC
до пересечения с окружностью в точке C_{1}
. Тогда
\angle BC_{1}D+\angle BAD=180^{\circ}
(свойство вписанного четырёхугольника). Поэтому \angle BCD=\angle BC_{1}D
. Поскольку BCD
— внешний угол треугольника CBB_{1}
, то
\angle BCD=\angle BC_{1}D+\angle CBC_{1},
что невозможно.
Если точка C
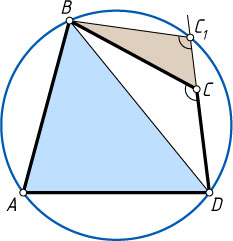
окажется вне окружности, то все сложней. Если считать известным, что одна из сторон CD
или BC
(например, CD
) пересекает окружность в некоторой точке C_{1}
так, что получился вписанный четырёхугольник ABC_{1}D
(см. рис.), поэтому
\angle BC_{1}D+\angle BAD=180^{\circ}.
Тогда
\angle BC_{1}D=180^{\circ}-\angle BAD=\angle BCD,
что противоречит теореме о внешнем угле треугольника, т. е. равенству
\angle BCD=\angle BC_{1}D+\angle CBC_{1}.
Второй способ (для случая, когда точка C
оказалась вне окружности). Заметим, что сумма углов любого четырёхугольника равна 360^{\circ}
, поэтому, если сумма одной пары его углов больше 180^{\circ}
, то сумма второй меньше 180^{\circ}
.
Отметим точку C'
лежащую одновременно на окружности и внутри четырёхугольника ABCD
. Тогда
\angle C'DA\lt\angle CDA~\mbox{и}~\angle C'BA\lt\angle CBA,
поэтому
\angle C'DA+\angle C'BA\lt\angle CDA+\angle CBA=180^{\circ}.
Тогда
\angle BCD+\angle BAD\gt180^{\circ},
Что противоречит условию.
Аналогично для случая, когда точка C
окажется внутри описанной окружности треугольника ABD
.
Примечание. См. статью Д.Терёшина «Вписанный четырёхугольник», Квант, 1992, N2, с.37-39.
Источник: Шень А. Х. Геометрия в задачах. — М.: МЦНМО, 2013. — № 488 и № 489, с. 145-146
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 80
Источник: Колмогоров А. Н. и др. Геометрия: Учебное пособие для 8 кл. средней школы. — 3-е изд. — М.: Просвещение, 1975. — с. 44
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 729, с. 182
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 594
