54. Отрезки AB
и CD
— диаметры одной окружности. Из точки M
этой окружности опущены перпендикуляры MP
и MQ
на прямые AB
и CD
. Докажите, что длина отрезка PQ
не зависит от положения точки M
.
Указание. Центр данной окружности и точки P
, M
, Q
лежат на окружности, диаметр которой равен радиусу данной окружности.
Решение. Первый способ. Если O
— центр данной окружности, а R
— её радиус, то точки P
, M
, Q
, O
лежат на окружности с диаметром MO=R
. Поэтому
PQ=MO\sin\angle AOD=R\sin\angle AOD.
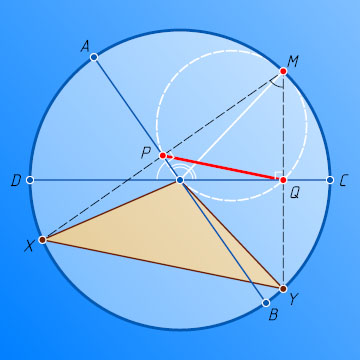
Второй способ. Пусть X
и Y
— точки, симметричные точке M
относительно прямых AB
и CD
соответственно. Тогда X
и Y
принадлежат данной окружности и PQ
— средняя линия треугольника MXY
. Поэтому XY=2PQ
, а XY
— основание равнобедренного треугольника (с вершиной в центре окружности) с постоянными боковыми сторонами (радиусами окружности) и с постоянным углом между ними.
Источник: Московская математическая олимпиада. — 1958, XXI, 1-й тур, 7 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 2, с. 62
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.32, с. 34
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.33, с. 34
