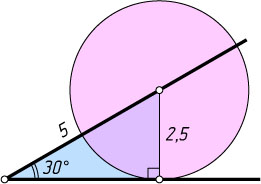
56. Дан угол в 30^{\circ}
. Постройте окружность радиуса 2,5, касающуюся одной стороны этого угла и имеющую центр на другой его стороне. Найдите расстояние от центра окружности до вершины угла.
Ответ. 5.
Указание. Катет прямоугольного треугольника, лежащий против угла в 30^{\circ}
, равен половине гипотенузы.
Решение. Поскольку катет прямоугольного треугольника, лежащий против угла в 30^{\circ}
, равен половине гипотенузы, расстояние от центра окружности до вершины угла равно 5.
С центром в точке, удалённой от вершины угла на расстояние, равное 5, проводим окружность радиуса 2,5.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 30, с. 31
