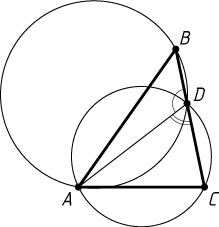
60. Через вершины A
и B
треугольника ABC
проходит окружность радиуса r
, пересекающая сторону BC
в точке D
. Найдите радиус окружности, проходящей через точки A
, D
и C
, если AB=c
и AC=b
.
Ответ. \frac{br}{c}
.
Указание. \sin\angle ADC=\sin\angle ADB
.
Решение. Поскольку
\angle ADC+\angle ADB=180^{\circ},
то
\sin\angle ADC=\sin\angle ADB=\frac{c}{2r}.
Если R
— радиус окружности, проходящей через точки A
, C
и D
, то b=2R\sin\angle ADC
. Отсюда находим, что
R=\frac{b}{2\sin\angle ADC}=\frac{b}{2\cdot\frac{c}{2r}}=\frac{br}{c}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 94, с. 14
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 94, с. 13
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.20, с. 87
