62. В четырёхугольнике ABCD
, вписанном в окружность, биссектрисы углов A
и B
пересекаются в точке E
, лежащей на стороне CD
. Известно, что \frac{CD}{BC}=m
. Найдите:
1) отношение расстояний от точки E
до прямых AD
и BC
;
2) отношение площадей треугольников ADE
и BCE
.
Ответ. 1) 1; 2) m-1
.
Указание. Докажите, что DC=AD+BC
.
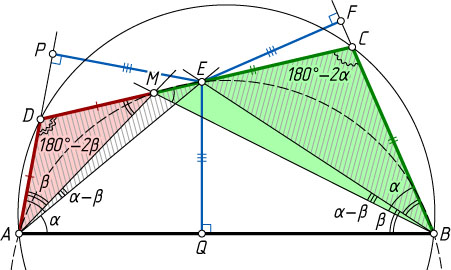
Решение. Докажем, что DC=AD+BC
. Пусть \angle A=2\alpha
, \angle B=2\beta
, \alpha\gt\beta
, а биссектрисы углов A
и B
пересекаются в точке E
, лежащей на стороне CD
.
От луча AD
в полуплоскость, содержащую точку E
, отложим луч под углом \beta
. Поскольку \beta\lt\alpha
, этот луч проходит между сторонами угла DAE
, поэтому он пересекает сторону CD
в некоторой точке M
, лежащей между D
и E
,
\angle AMD=180^{\circ}-\angle DAM-\angle ADC=180^{\circ}-\angle DAM-(180^{\circ}-\angle ABC)=180^{\circ}-\beta-(180^{\circ}-2\beta)=\beta.
Поэтому треугольник ADM
— равнобедренный, AD=DM
, а \angle AMC=180^{\circ}-\beta
. Значит, точки A
, M
, E
и B
лежат на одной окружности.
Следовательно,
\angle MBE=\angle MAE=\alpha-\beta,~\angle MBC=\angle MBE+\angle CBE=(\alpha-\beta)+\beta=\alpha.
Тогда
\angle BMC=180^{\circ}-\angle MBC-\angle BCD=180^{\circ}-\alpha-(180^{\circ}-2\alpha)=\alpha.
Поэтому треугольник BMC
— также равнобедренный, BC=MC
. Следовательно,
AD+BC=DM+MC=DC.
Пусть теперь P
, Q
и F
— проекции точки E
на прямые AD
, AB
и BC
соответственно. Поскольку лучи AE
и BE
— биссектрисы углов DAE
и ABC
, то EP=EQ=EF
. Следовательно, \frac{EP}{EF}=1
.
Поскольку AD+BC=DC
и \frac{DC}{BC}=m
, то \frac{AD}{BC}=m-1
. Следовательно,
\frac{S_{\triangle ADE}}{S_{\triangle BCE}}=\frac{AD}{BC}=m-1.
Источник: Вступительный экзамен на физический факультет МГУ. — 1981, вариант 1, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 33
