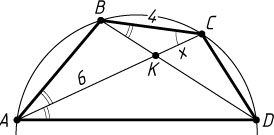
65. Четырёхугольник ABCD
вписан в окружность. Диагональ AC
является биссектрисой угла BAD
и пересекается с диагональю BD
в точке K
. Найдите KC
, если BC=4
, а AK=6
.
Ответ. 2.
Указание. Треугольник KBC
подобен треугольнику BAC
.
Решение. Поскольку
\angle KBC=\angle DBC=\angle DAC=\angle BAC,
то треугольник KBC
подобен треугольнику BAC
(по двум углам). Поэтому KC:BC=BC:AC
.
Пусть KC=x
. Тогда
\frac{x}{4}=\frac{4}{x+6}.
Из этого уравнения находим, что x=2
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1981 (отделение общей геологии), вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 90
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.26, с. 113
