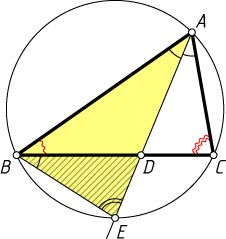
67. В треугольнике ABC
даны углы B
и C
. Биссектриса внутреннего угла BAC
пересекает сторону BC
в точке D
, а окружность, описанную около треугольника ABC
, — в точке E
. Найдите отношение AE:DE
.
Ответ. \frac{\cos^{2}\frac{C-B}{2}}{\cos^{2}\frac{C+B}{2}}
.
Указание. Докажите, что треугольник BDE
подобен треугольнику ABE
. Примените формулу a=2R\sin\alpha
.
Решение. Поскольку
\angle DBE=\angle CBE=\angle CAE=\angle BAE,
то треугольник BDE
подобен треугольнику ABE
. Тогда
\frac{DE}{BE}=\frac{BE}{AE},~DE=\frac{BE^{2}}{AE}.
Пусть R
— радиус окружности. По формуле a=2R\sin\alpha
выразим отрезки AE
и BE
через R
, \angle B
и \angle C
:
AE=2R\sin\angle ABE=2R\sin\left(B+\frac{1}{2}A\right)=
=2R\sin\left(B+90^{\circ}-\frac{1}{2}B-\frac{1}{2}C\right)=2R\cos\left(\frac{1}{2}C-\frac{1}{2}B\right),
BE=2R\sin\angle BAE=2R\sin\frac{1}{2}A=
=2R\sin\left(90^{\circ}-\frac{1}{2}B-\frac{1}{2}C\right)=2R\cos\left(\frac{1}{2}C+\frac{1}{2}B\right).
Следовательно,
\frac{AE}{DE}=\frac{AE^{2}}{BE^{2}}=\frac{\cos^{2}\left(\frac{1}{2}C-\frac{1}{2}B\right)}{\cos^{2}\left(\frac{1}{2}C+\frac{1}{2}B\right)}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1969, № 4, вариант 6
