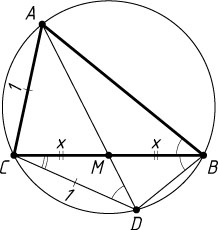
68. Продолжение медианы треугольника ABC
, проведённой из вершины A
, пересекает описанную около треугольника ABC
окружность в точке D
. Найдите BC
, если AC=DC=1
.
Ответ. \sqrt{2}
.
Указание. Пусть M
— середина BC
. Тогда треугольник DCM
подобен треугольнику BCD
.
Решение. Пусть M
— середина BC
. Поскольку \angle ADC=\angle ABC=\angle CBD
, то треугольник DCM
подобен треугольнику BCD
по двум углам. Следовательно, \frac{DC}{BC}=\frac{CM}{DC}
.
Обозначим BM=CM=x
. Тогда \frac{1}{2x}=\frac{x}{1}
. Отсюда находим, что x^{2}=\frac{1}{2}
. Следовательно, BC=2x=\sqrt{2}
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1985, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 85
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.27, с. 113
